FONCTIONS ANALYTIQUES - Représentation conforme

FONCTIONS ANALYTIQUES - Représentation conforme

La représentation conforme la plus anciennement connue est la projection stéréographique, inventée par les Grecs (Hipparque, Ptolémée). Les problèmes cartographiques conduisirent à la découverte d’autres applications conservant les angles d’un domaine sphérique sur un domaine plan, telle la projection de Mercator (XVI^e siècle). Au début du XIX^e siècle, Carl Friedrich Gauss étudia systématiquement les propriétés intrinsèques des surfaces de l’espace habituel; en particulier, il examina les applications bijectives d’une surface sur une autre qui sont différentiables, ainsi que leur réciproque, et qui conservent les angles. La notion de représentation conforme reçut un nouvel éclairage avec l’avènement de la théorie des fonctions d’une variable complexe, à laquelle elle est intimement liée. Bernhard Riemann sut exploiter cette relation de façon particulièrement féconde, introduisant la notion de surface de Riemann , qui résout les difficultés dues aux «fonctions multiformes» et donne un cadre convenable à la théorie du prolongement analytique. Cette théorie pose un certain nombre de problèmes topologiques qui ont conduit Bernhard Riemann et Henri Poincaré à développer les premières bases de la topologie algébrique.

1. Définition

La représentation conforme

Considérons un domaine D du plan R². On dit qu’une application différentiable f de D dans R² est conforme en un point z ⁰ de D si sa dérivée (ou application linéaire tangente) D¹ f (z ⁰) en z ⁰ conserve les angles orientés (cf. CALCUL INFINITÉSIMAL – Calcul à plusieurs variables). En convenant que l’angle en z ⁰ de deux chemins différentiables 塚¹ et 塚² passant par z ⁰ est l’angle de leurs tangentes en z ⁰, on voit que cette condition revient à la suivante: l’angle orienté en f (z ⁰) des chemins images f 獵 塚¹ et f 獵 塚² est égal à l’angle orienté de 塚¹ et 塚² en z ⁰, quels que soient les chemins 塚¹ et 塚² différentiables passant par z ⁰ (fig. 1).

On sait qu’une application linéaire du plan dans lui-même, qui conserve les angles orientés est une similitude directe de centre O. Ainsi, la conformité de f en z ⁰ signifie que l’application linéaire tangente D¹f (z ⁰) est une similitude directe. Il est très commode de représenter les similitudes à l’aide de la multiplication des nombres complexes. Dans la suite, on considérera que le plan est le corps des nombres complexes C, et l’on écrira x + iy pour le point (x , y ) du plan (cf. nombres COMPLEXES); une similitude directe de centre O est alors une application de la forme z 料 az , où a est un nombre complexe non nul dont le module et l’argument sont respectivement le rapport et l’angle de la similitude; dans la base canonique (1, i ) de C sur R, la matrice de la similitude considérée s’écrit:

où 見 est la partie réelle de a , et 廓 sa partie imaginaire.

Dire que f est conforme en z ⁰ revient donc à dire que sa dérivée est de la forme h 料 ah , avec a 捻 C, a 0; par conséquent, le rapport:

tend vers 0 avec h , ou encore f est dérivable au sens complexe en z ⁰, avec comme dérivée, f (z ⁰) = a 0 (cf. FONCTIONS ANALYTIQUES – Fonctions analytiques d’une variable complexe, chap. 2). En termes réels, on doit écrire que la matrice jacobienne de f = P + i Q, soit:

est de la forme:

ce qui donne les conditions de Cauchy-Riemann: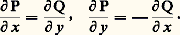

Ainsi toute fonction holomorphe f dans D, dont la dérivée ne s’annule pas, est conforme en tout point de D. Or on peut montrer que l’image d’une partie ouverte de C par une fonction holomorphe non constante est ouverte; l’image du domaine D par une fonction holomorphe non constante f est donc un domaine f (D). De plus, si f est injective (on dit quelquefois univalente), sa dérivée ne s’annule pas; f définit une bijection de D sur f (D) dont l’application réciproque est holomorphe dans f (D); f est alors une représentation conforme de D sur f (D). Les domaines D et f (D) sont dits conformément équivalents, ou encore isomorphes; en ce qui concerne la théorie des fonctions analytiques, ils ont les mêmes propriétés, car l’application: g 料 g 獵f est une bijection de l’ensemble des fonctions holomorphes dans f (D) sur l’ensemble des fonctions holomorphes dans D. Enfin, si g est une représentation conforme de f (D) sur un nouveau domaine D , la composée g 獵f est une représentation conforme de D sur D .

Exemples de représentations conformes

Chaque fonction holomorphe injective dans un domaine D définit une représentation conforme de D sur f (D). Par exemple, la fonction z 料 z ² est holomorphe et injective dans le demi-plan supérieur , défini par Im z 礪 0; son image est le complémentaire dans C de R⁺ (ensemble des nombres réels strictement positifs), c’est-à-dire le plan fendu suivant le demi-axe réel positif. Comme: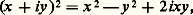

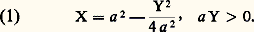on voit que l’image de la demi-droite x = a (a 0), y 礪 0 est la demi-parabole:

La parabole (1) admet l’axe réel pour axe de symétrie; son foyer est en O et son sommet d’ordonnée positive. L’image de la demi-droite x = 0, y 礪 0 est le demi-axe réel négatif. De plus, la droite y = b (b 礪 0) est

transformée en la parabole:

qui a pour axe l’axe réel; son foyer est en O et son sommet d’ordonnée négative. Les paraboles de la famille (1) sont évidemment toutes orthogonales à celles de la famille (2) (fig. 2). Remarquons que l’application conforme considérée se prolonge continûment à la frontière y = 0 du domaine (en fait z 料 z ² est holomorphe dans le plan tout entier, mais non injective); l’image de cette frontière est la frontière du domaine image (le demi-axe réel positif).

Par restriction de la représentation conforme précédente, on obtient une représentation conforme du demi-plan y 礪 b sur l’extérieur d’une parabole.

On peut étudier de la même façon la fonction holomorphe z 料 z ⁿ (n entier 礪 0), qui est injective dans le secteur angulaire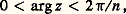

et définit une représentation conforme de ce secteur angulaire, sur le plan fendu suivant l’axe réel positif. Ici encore, la représentation se prolonge par continuité à la frontière, mais, au point O, la transformation cesse d’être conforme, car la dérivée s’annule; chaque angle en O est multiplié par n dans cette transformation.

Les applications réciproques de ces représentations conformes fournissent de nouveaux exemples: dans le plan fendu suivant le demi-axe réel positif, on définit sans ambiguïté la fonction z 料 z ^1/n par la condition:

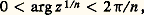et on obtient une représentation conforme du plan fendu sur un secteur angulaire d’amplitude 2 神/n . Pour tout exposant 見 réel 礪 0, on peut définir une représentation conforme z 料 z size=1^見 dans le secteur angulaire:

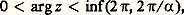en imposant la condition:

qui détermine une branche holomorphe de la fonction considérée, injective dans le secteur décrit par z ; l’image de cette représentation conforme est le secteur angulaire: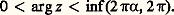

En composant de telles représentations conformes, on peut construire une représentation conforme d’un secteur angulaire quelconque sur un autre, par exemple sur le demi-plan supérieur. Pour préciser la représentation z 料 z ^1/2 du plan fendu sur le demi-plan supérieur, décrivons les transformées des droites parallèles aux axes. L’image de la droite x = a (a 0) est la demi-hyperbole équilatère:

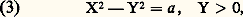dont les asymptotes sont les bissectrices des axes de coordonnées; si a 礪 0, les sommets sont sur l’axe réel et l’image est formée de la moitié supérieure de chacune des branches de l’hyperbole; si, au contraire, a 麗 0, les sommets sont sur l’axe imaginaire et l’image est la branche supérieure de l’hyperbole. La droite x = 0 a pour image la réunion des deux demi-bissectrices des axes qui sont dans le demi-plan supérieur. Enfin, la droite y = b (b 0) est transformée en la branche supérieure de l’hyperbole équilatère:

dont les asymptotes sont les axes de coordonnées et la demi-droite y = 0, x 麗 0 est transformée en la demi-droite X = 0, Y 礪 0. Chaque hyperbole de la famille (4) est orthogonale à toutes les hyperboles de la famille (3) (fig. 3). Le demi-plan y 礪 b est représenté conformément sur l’intérieur d’une branche d’hyperbole.

Étudions maintenant la représentation conforme définie par la fonction z 料 1/z , qui est holomorphe et injective dans C 漣0 et admet pour image C 漣0; cette transformation est sa propre réciproque (transformation involutive).

Ici: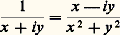

et les droites x = a (a 0) et y = b (b 0) sont respectivement transformées en les cercles passant par O (privés de O):

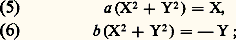les cercles (5) sont orthogonaux aux cercles (6); ils sont centrés sur l’axe réel et tangents en O à l’axe imaginaire (fig. 4). Les droites x = 0 et y = 0 sont globalement invariantes. Plus généralement, chaque droite issue de O est transformée en sa symétrique par rapport à l’axe réel; en composant avec la symétrie d’axe R, on obtient une transformation z 料 1/ 磻 , appelée inversion (de pôle O et de puissance 1), qui laisse globalement invariante chaque droite issue de O; elle transforme les angles en leurs opposés. De cette transformation se déduit par restriction une représentation conforme du demi-plan y 礪 b sur le disque b (X² + Y²) + Y 麗 0; en composant à droite avec la translation z 料 z + ib et à gauche avec la similitude z 料 1 漣 2 biz , on trouve une représentation conforme:

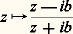du demi-plan supérieur y 礪 0 sur le disque unité |z | 麗 1 (on peut prendre b = 1); cette transformation se prolonge à la frontière, l’image de la droite y = 0 étant le cercle unité privé du point 漣 1. Il est maintenant possible de construire une représentation conforme d’un secteur angulaire quelconque sur le disque unité, puisqu’un tel secteur se représente conformément sur le demi-plan.

La fonction z 料 e ^z donne un nouvel exemple de représentation conforme ^{[cf. EXPONENTIELLE ET LOGARITHME]}. Elle est holomorphe dans tout le plan et sa restriction à la bande 0 麗 Im z 麗 2 神 est injective; l’image de cette bande est le plan fendu suivant le demi-axe réel positif. Comme e ^z = e ^x+iy = e ^x e ^iy , c’est-à-dire |e ^z | = e ^z et arg e ^z = y , nous décrirons l’image à l’aide des coordonnées polaires r et (0 麗 麗 2 神). Les segments x = constante de la bande sont transformés en cercles de centre O (privés du point réel 礪 0); les droites y = constante sont transformées en demi-droites passant par O (fig. 5). La transformation réciproque, notée lg, représente le plan fendu conformément sur une bande.

La fonction:

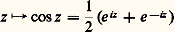est composée des fonctions:

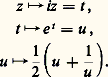Étudions d’abord la dernière fonction: elle est holomorphe dans le plan privé de O, et prend la même valeur aux points u et 1/u ; restreinte à l’extérieur |u | 礪 1 du disque unité, elle est injective et représente conformément l’extérieur du disque unité sur le plan privé de l’image du cercle unité, c’est-à-dire le plan privé du segment d’extrémité 漣 1 et 1. Si u = re ⁱ size=1 (r 礪 1), les coordonnées de son image sont:

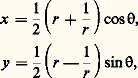les cercles de centre O sont donc transformés en ellipses de foyers 漣 1 et 1, tandis que les droites passant par O sont transformées en hyperboles ayant les mêmes foyers, avec dégénérescence en les axes de coordonnées (fig. 6). La même fonction donne une représentation conforme du disque unité privé de son centre sur le plan privé du segment d’extrémités 漣 1 et 1.

Il est maintenant facile de voir que la fonction cos définit une représentation conforme de la demi-bande 0 麗 Re z 麗 2 神, Im z 礪 0 sur le plan privé de la demi-droite Im z = 0, Re z 礪 漣 1 (fig. 7).

2. Le problème de la représentation conforme

Étant donné des domaines D et D du plan, sont-ils conformément équivalents? Dans l’affirmative, il s’agira de construire, au moins d’une manière approchée, une représentation conforme de D sur D . Ce problème a des applications en diverses questions de physique (par exemple en hydrodynamique), car il permet de résoudre certains problèmes de Dirichlet: pour trouver une fonction harmonique u , connaissant une courbe u = a (constante, qui est la frontière d’un domaine D conformément équivalent au demi-plan supérieur, on utilise une représentation conforme f de D sur le demi-plan supérieur; si f se prolonge par continuité à la frontière de D et transforme cette frontière en celle du demi-plan, soit la droite Im z = 0, la solution est u = Im (f + a ) ^{[cf. POTENTIEL ET FONCTIONS HARMONIQUES]}.

Si les domaines D et D sont conformément équivalents, ils sont homéomorphes , c’est-à-dire qu’il existe une bijection continue de D sur D dont la réciproque est aussi continue. Ainsi est réalisée une condition nécessaire d’isomorphisme; mais cette condition n’est pas suffisante, car le plan C et le disque unité sont homéomorphes (l’application z 料 z /(1 + |z |) est un homéomorphisme du premier sur le second), mais certainement pas isomorphes, puisque la fonction z 料 z est holomorphe et bornée dans le disque unité, alors que toute fonction holomorphe et bornée dans C est constante d’après le théorème de Liouville (cf. FONCTIONS ANALYTIQUES – Fonctions analytiques d’une variable complexe).

D’ailleurs, comme on l’a vu ci-dessus, une grande variété de domaines sont conformément équivalents au disque unité: le demi-plan, un secteur angulaire, une bande ou une demi-bande, l’extérieur d’une parabole. En fait, Riemann a obtenu (par une démonstration un peu incomplète) le remarquable résultat suivant: Tout domaine D différent du plan C et simplement connexe (c’est-à-dire que tout lacet de D peut se déformer continûment dans D en un point) est conformément équivalent au disque unité.

Ce théorème a été complètement démontré par W. F. Osgood, puis par P. Koebe, qui l’a généralisé en donnant aussi des modèles pour les domaines non simplement connexes à l’aide du disque unité privé d’un certain nombre d’arcs de cercles de centre O. Voici les étapes de la démonstration:

a ) On commence par se ramener au cas où D est borné en construisant une fonction holomorphe bornée et injective dans D (c’est assez facile). Il est alors possible de trouver des représentations conformes de D sur des domaines contenus dans le disque unité (à l’aide de similitudes, par exemple).

b ) En choisissant un point a de D et en considérant l’ensemble F des représentations conformes de D sur des parties du disque unité qui transforment a en O, on démontre que, pour un élément f de F, les propriétés suivantes sont équivalentes: (I) L’image de D par f est le disque unité. (II) |f (a )| est maximale parmi les valeurs que ce nombre peut prendre lorsque f parcourt F.

c ) Il reste à démontrer l’existence d’un élément f de F qui réalise le maximum de |f (a )|. Cela résulte du fait que F est un ensemble compact pour la «topologie de la convergence compacte» dans D et que f 料 |f (a )| est une fonction numérique continue dans F.

En général, on ne peut pas déterminer explicitement une représentation conforme de D sur le disque unité, mais seulement chercher à construire des approximations d’une telle représentation; c’est un problème d’analyse numérique qui peut être difficile. La méthode de H. A. Schwarz donne explicitement une représentation conforme du demi-plan supérieur sur un polygone convexe arbitraire par une formule du type:

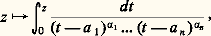où les nombres a ⁱ sont réels et les exposants 見ⁱ compris entre 0 et 1 et de somme 2; pour n = 4 et 見¹ = 見² = 見³ = 見⁴ = 1/2, l’intégrale considérée est une intégrale elliptique et donne une représentation conforme du demi-plan sur un rectangle (cf. FONCTIONS ANALYTIQUES – Fonctions elliptiques et modulaire).

Il est possible de déterminer toutes les représentations conformes du plan sur lui-même ou du disque unité sur lui-même. Dans le cas du plan, une représentation conforme f : CC est une fonction entière qui est injective; cela entraîne d’abord que f est un polynôme, sinon la fonction u 料 f (1/u ) aurait une singularité essentielle à l’origine et transformerait le disque unité (privé de O) en un ensemble partout dense dans C d’après un théorème de Weierstrass; ainsi, l’image par f de l’extérieur du disque unité serait partout dense et, par suite, rencontrerait l’image du disque unité, qui est un ouvert: c’est impossible si f est injective. De plus, f doit être de degré 1, car un polynôme de degré n a n racines; donc f est de la forme f (z ) = az + b (a 0) et la représentation conforme est une similitude. Il est remarquable que les transformations du plan en lui-même qui conservent les angles conservent la distance euclidienne à un facteur près; ces transformations forment un groupe à quatre paramètres, opérant transitivement.

Passons au cas du disque unité, en étudiant d’abord les automorphismes laissant fixe le point O. Un tel automorphisme est en particulier une fonction holomorphe f telle que f (0) = 0 et |f (z )| 麗 1 pour tout point z du disque unité; le lemme de Schwarz lui est applicable: |f (z )| 諒 |z |, avec égalité seulement si f (z ) est proportionnel à z (cf. FONCTIONS ANALYTIQUES – Fonctions analytiques d’une variable complexe); le même lemme appliqué à f ^-1 donne |z | 諒 |f (z )|, donc l’égalité a lieu et f (z ) = az avec une constante a de module 1. Si f est un automorphisme quelconque du disque unité, on pose b = f ^-1(0). L’application:

est une représentation conforme du disque sur lui-même qui transforme 0 en b . Donc f 獵 g , qui est conforme et laisse O fixe, est une rotation z 料 az (|a | = 1), et: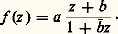

Les automorphismes du disque unité sont ainsi les transformations homographiques qui le laissent invariant; ils forment un groupe à trois paramètres transitif dans le disque unité. On peut montrer qu’il existe une métrique riemannienne dans le disque unité qui est invariante par ce groupe; sa courbure est constante et négative de sorte que la géométrie correspondante est celle de N. I. Lobatchevsky (c’est le fameux modèle de Poincaré pour la géométrie non euclidienne).

Les résultats obtenus pour le disque unité se transposent au demi-plan. Comme le passage de l’un à l’autre s’opère au moyen d’une transformation homographique, les automorphismes du demi-plan supérieur sont les transformations homographiques qui le laissent invariant:

avec a , b , c , d réels et ad 漣 bc 礪 0.

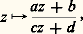3. Surfaces de Riemann

Projection stéréographique et sphère de Riemann

Considérons la sphère S² de centre O et de rayon 1 dans l’espace R³ (où les coordonnées sont notées x , y , t ). La projection stéréographique de pôle (0, 0, 1) sur le plan t = 0 est l’application qui, à chaque point (x , y , t ) de la sphère distinct de (0, 0, 1), associe le point où la droite joignant (0, 0, 1) à (x , y , t ) rencontre le plan t = 0 (fig. 8).

Ainsi, l’image de (x , y , t ) est le point:

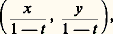soit:

avec la notation complexe. Il est facile de montrer que cette application conserve les angles (c’est-à-dire que l’application linéaire tangente possède cette propriété). C’est une représentation conforme de la sphère privée du pôle (0, 0, 1) sur le plan C.

On peut aussi considérer la projection stéréographique de pôle (0, 0, 漣 1), qui s’écrit: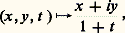

et représente conformément la sphère privée de (0, 0, 漣 1) sur C. Il n’a pas été tenu compte des questions d’orientation et un même angle orienté sur la sphère est transformé en des angles opposés par les deux projections; ce défaut se corrige en composant la deuxième projection avec la symétrie d’axe réel, ce qui donne la représentation conforme:

de la sphère privée de (0, 0, 漣 1) sur C. Si z et z sont les images d’un même point (x , y , t ) distinct de (0, 0, 1) et de (0, 0, 漣 1) par nos deux représentations, alors:

ainsi on passe de l’une à l’autre par la transformation z 料 1/z .

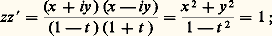Si D est une partie ouverte de la sphère, la première projection stéréographique identifie D privé éventuellement du pôle (0, 0, 1) à un ouvert D de C, tandis que la seconde projection identifie D privé éventuellement de (0, 0, 漣 1) à un autre ouvert D du plan. On dira qu’une fonction numérique complexe f définie dans D est holomorphe si les fonctions correspondantes dans D et D sont holomorphes; cette définition est cohérente parce que la transformation z 料 1/z est un isomorphisme de D privé éventuellement de l’origine sur D privé éventuellement de l’origine. Avec cette notion de fonction holomorphe, la sphère S² s’appelle sphère de Riemann. Le plan s’identifie par la projection stéréographique de pôle (0, 0, 1) au complémentaire de (0, 0, 1) dans la sphère de Riemann; comme ce point a pour image O par l’autre projection, il s’appellera point à l’infini noté 秊 (prolongeant ainsi z 料 1/z en posant 1/0 = 秊). La sphère de Riemann, ainsi considérée comme C complété par un point à l’infini, peut aussi s’identifier à la droite projective complexe P¹(C).

Pour déterminer les automorphismes de la sphère de Riemann, remarquons d’abord que ceux qui laissent fixe le point à l’infini donnent par restriction des automorphismes de C, c’est-à-dire des similitudes: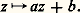

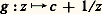Si f est un automorphisme quelconque, posons c = f ^-1(face=F0019 秊); l’application:

transforme 秊 en c et c’est un automorphisme de la sphère de Riemann, donc f 獵 g laisse 秊 fixe et c’est encore un automorphisme; il en résulte que f 獵 g est une similitude z 料 az + b et que:

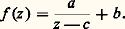Les représentations conformes de la sphère de Riemann sur elle-même sont donc les transformations homographiques:

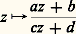(a , b , c , d complexes tels que ad 漣 bc 0). Elles forment un groupe à six paramètres réels et transforment les cercles en cercles (groupe circulaire).

Courbes analytiques et surfaces de Riemann

La structure qui a été définie précédemment sur la sphère s’exprime bien dans le langage des variétés ^{[cf. VARIÉTÉS DIFFÉRENTIABLES]}.

D’une manière générale, on appelle variété analytique complexe de dimension 1, ou courbe analytique complexe (régulière), ou encore, par abus de langage, surface de Riemann, un espace topologique séparé X muni d’un atlas analytique complexe maximal à valeurs dans des ouverts de C. Cette définition repose sur la notion de carte de X à valeur dans un ouvert de C: il s’agit d’un homéomorphisme d’un ouvert de X sur un ouvert de C; deux cartes dont les ouverts de définition se rencontrent définissent un homéomorphisme appelé changement de carte entre les deux images de l’intersection des ouverts de définition. Un atlas analytique complexe est une famille de cartes dont les ouverts de définition recouvrent X et tel que tous les changements de cartes (entre des cartes de la famille) soient holomorphes; par exemple, la projection stéréographique de pôle (0, 0, 1) et celle de pôle (0, 0, 漣 1) composée avec la symétrie d’axe R sont des cartes de S² et le changement de cartes est z 料 1/z ; ces cartes forment un atlas analytique complexe de S² qui définit une structure de courbe analytique complexe sur la sphère (droite projective complexe). Voici encore un exemple important dans la théorie des fonctions elliptiques: étant donné deux nombres 諸 et 諸 dont le rapport n’est pas réel, considérons le quotient X de C par le sous-groupe engendré par 諸 et 諸 ; muni de la topologie quotient de celle de C, c’est un espace séparé (homéomorphe au tore T²) sur lequel on définit un atlas analytique complexe à l’aide des ouverts de C assez petits pour que l’application canonique 神 de C sur X y soit injective, en prenant pour cartes les réciproques des restrictions de 神 à de tels ouverts; X devient ainsi une courbe analytique complexe (courbe elliptique).

Comme une fonction holomorphe est a fortiori différentiable (au sens réel), tout atlas analytique complexe est aussi un atlas différentiable et définit une structure de variété différentiable de dimension réelle 2. Une courbe analytique complexe possède donc une structure de surface différentiable; cette surface est orientable et triangulable (la dernière propriété est due à T. Radó, 1925; cf. TOPOLOGIE - Topologie algébrique).

On démontre qu’une surface orientable triangulable connexe et compacte est homéomorphe soit à la sphère S², soit à une «sphère à p anses» (ou «tore à p trous») obtenue en identifiant deux à deux les côtés d’un polygone à 4 p côtés selon le symbole:

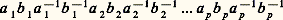(où les 4 p côtés sont nommés dans l’ordre où ils se présentent sur le bord orienté du polygone, a ^1-1 devant être identifié à a ¹ après avoir renversé son orientation, etc., fig. 9). Chaque côté du polygone devient un lacet sur la surface et les classes d’homotopie des 2 p lacets ainsi obtenus engendrent le groupe fondamental de cette surface; l’entier p s’appelle le genre topologique de la surface. La sphère S² est simplement connexe; on lui attribue le genre 0. Le tore T² est de genre 1. Ces résultats s’appliquent aux courbes analytiques complexes connexes et compactes.

Tout ouvert d’une courbe analytique complexe est muni d’une manière naturelle d’une structure induite qui en fait aussi une variété analytique complexe de dimension 1. Plus généralement, si X est une courbe analytique complexe et si f : X 料 X est un homéomorphisme local, l’espace X a une structure naturelle de courbe analytique complexe provenant de celle de X. Cela s’applique au revêtement universel 黎X de X; par exemple, le revêtement universel d’une courbe elliptique est C.

La notion de fonction holomorphe sur une courbe analytique complexe se définit en procédant comme ci-dessus pour la sphère de Riemann. Plus généralement, on peut définir la notion d’application holomorphe d’une courbe analytique complexe dans une autre.

Deux courbes analytiques sont dites isomorphes ou conformément équivalentes s’il existe un homéomorphisme holomorphe de l’une sur l’autre; il est facile de voir que l’application réciproque d’un tel homéomorphisme est aussi holomorphe. Le théorème de représentation conforme de Riemann se généralise ainsi:

Toute courbe analytique complexe connexe et simplement connexe est isomorphe à l’une des suivantes:

a ) La sphère de Riemann (droite projective complexe);

b ) Le plan C (droite affine complexe);

c ) Le disque unité (ou le demi-plan).

On distingue aisément les cas a , b , c , car la sphère est la seule à être compacte, et le disque unité le seul à admettre des fonctions holomorphes bornées non constantes. Le revêtement universel d’une courbe analytique complexe connexe X est isomorphe à l’une des courbes précédentes; si c’est la sphère, la courbe X est elle-même isomorphe à la sphère; si c’est le plan, alors X est isomorphe au plan ou au plan privé d’un point, ou bien est une courbe elliptique.

Une application holomorphe non constante f : X 料 Y est toujours ouverte. Ses fibres f ^-1(y ) (y 捻 Y) sont discrètes et, pour tout point x 捻 X, il existe des cartes 﨏 et 祥 de X et Y définies respectivement dans des voisinages de x et de f (x ) telles que 﨏 (x ) = 0, 祥(f (x )) = 0 et que 祥 獵 f 獵 﨏^-1 soit de la forme z 料 z ⁿ , où n est un entier 閭 1, que l’on appelle l’indice de ramification de f en x ; en général n = 1, et l’ensemble des points de X où l’indice de ramification est 閭 2 (points de ramification de f ) est discret. Par exemple, l’application z 料 z ² de C dans C est ramifié seulement en 0, avec 2 comme indice de ramification; si on la prolonge à la sphère de Riemann en posant 秊² = 秊, on obtient une application holomorphe de la sphère de Riemann sur elle-même, ramifiée en 0 et en 秊, et dont les fibres au-dessus des points 0, 秊 ont toutes 2 points. L’image réciproque, par cette application, du plan fendu C 漣 R⁺, se compose de 2 «feuillets» isomorphes au plan fendu (ils correspondent aux 2 déterminations de z ^1/2, fig. 10).

On appelle surface de Riemann une courbe analytique connexe X munie d’une application holomorphe non constante à valeurs dans la sphère de Riemann; ainsi (S², z 料 z ²) est une surface de Riemann, grâce à laquelle il est possible de prolonger analytiquement une branche holomorphe de la racine carrée: une telle branche est définie initialement dans le plan fendu, mais on peut la considérer comme définie dans l’un des 2 feuillets de la surface de Riemann (c’est alors l’application identique de la sphère de Riemann), ce qui permet de définir un prolongement analytique sur la surface de Riemann. D’une manière générale, le prolongement analytique d’une fonction holomorphe définie dans un ouvert de C conduit à construire une surface de Riemann sur laquelle on peut définir ce prolongement. Ainsi la fonction lg est définie sur la surface de Riemann (C, z 料 e ^z ), dont l’image est C 漣0; cette surface de Riemann n’est ramifiée en aucun point et a une infinité de feuillets. La surface de Riemann de la fonction algébrique y de x définie par l’équation: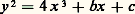

(avec b ³ + 27 c ² 0) est la courbe d’équation homogène:

dans le plan projectif complexe P²(C), munie de l’application dans la sphère de Riemann P¹(C), qui transforme le point (x , y , t ) en (x , t ) pour t 0 et le point (0, 1, 0) en (1, 0) = 秊 (coordonnées homogènes); elle a 2 feuillets et est ramifiée au-dessus des solutions de 4 x ³ + bx + c = 0; en paramétrant la courbe à l’aide des fonctions elliptiques x = face=F9828 p(u ), y = face=F9828 p (u ) (u 捻 C), on voit qu’elle est isomorphe au quotient de C par un sous-groupe discret de rang 2 (courbe elliptique, cf. FONCTIONS ANALYTIQUES – Fonctions elliptiques et modulaire).

Riemann a démontré que toute surface de Riemann compacte est la surface de Riemann d’une fonction algébrique. Autrement dit, toute courbe analytique complexe compacte est isomorphe à une courbe algébrique d’un certain espace projectif complexe ^{[cf. COURBES ALGÉBRIQUES]}. Il est remarquable que le genre topologique de la courbe analytique considérée est égal au genre algébrique de la courbe algébrique isomorphe; dans l’isomorphisme, les fonctions ou les formes différentielles méromorphes sur la courbe analytique s’identifient aux fonctions ou aux formes différentielles rationnelles sur la courbe algébrique.

Encyclopédie Universelle. 2012.